Paul Ehrenfest
Paul Ehrenfest is one of premier statistical mechanics of all time. Following in the footsteps of his advisor, and the father of statistical mechanics, Ludwig Boltzmann, Ehrenfest was renowned for his focus and clarity on fundamental problems.
The Ehrenfest Model
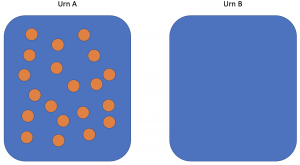
The Ehrenfest model, sometimes called the urn model or the dog-flea model, is a simple, discrete model for the exchange of gas molecules between two containers.
Consider two urns, A and B. Urn A contains ![]() marbles and urn B contains none. The marbles are labelled
marbles and urn B contains none. The marbles are labelled ![]() . In each step of the algorithm, a number between 1 and
. In each step of the algorithm, a number between 1 and ![]() is chosen randomly, with all values having equal probability. The marble corresponding to that value is moved to the opposite urn. Hence the first step of the algorithm will always involve moving a marble from A to B.
is chosen randomly, with all values having equal probability. The marble corresponding to that value is moved to the opposite urn. Hence the first step of the algorithm will always involve moving a marble from A to B.
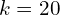 marbles.
marbles.To begin, the Markov chain will need to be defined. Define the random variable ![]() as the number of balls in urn A and the state space
as the number of balls in urn A and the state space ![]() and the probability of
and the probability of ![]() balls in urn A at step
balls in urn A at step ![]()
![]() .
.
The transition matrix looks:
![Rendered by QuickLaTeX.com \[P= \begin{blockarray}{cccccccccc} & 0 & 1 & 2 & 3 & \ldots & k-2 & k-1 & k\\ \begin{block}{c(cccccccc)} 0 & 0 & 1 & 0 & 0 & \ldots & 0 & 0 & 0 \\ 1 & \frac{1}{k} & 0 & \frac{k-1}{k} & 0 & \ldots & 0 & 0 & 0 \\ 2 & 0 & \frac{2}{k} & 0 & \frac{k-2}{k} & \ldots & 0 & 0 & 0 \\ 3 & 0 & 0 & \frac{3}{k} & 0 & \ldots & 0 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ k-2 & 0 & 0 & 0 & 0 & \ldots & 0 & \frac{k-(k-2)}{k} & 0\\ k-1 & 0 & 0 & 0 & 0 & \ldots & \frac{k-1}{k} & 0 & \frac{1}{k}\\ k & 0 & 0 & 0 & 0 & \ldots & 0 & 1 & 0 \end{block} \end{blockarray}\]](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-797f6854d1083354c1e3f2d48a3586dc_l3.png)
An important question for the Ehrenfest model is “what is the long term probability that there are ![]() balls in Urn A”.
balls in Urn A”.
Stationary distribution using induction
Let, ![]() , be the stationary distribution and
, be the stationary distribution and ![]() is the long term probability of
is the long term probability of ![]() balls in urn A. The three fundamental equations for finding a stationary distribution are,
balls in urn A. The three fundamental equations for finding a stationary distribution are,
(1) 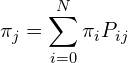
(2) 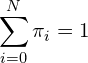
and,
(3) ![]()
For this problem there’s an easy way to solve it using the fact that ![]() and that
and that ![]() is a vector of the same state space
is a vector of the same state space ![]() , but not necessarily a probability vector, and that
, but not necessarily a probability vector, and that ![]() , where
, where ![]() is a constant and
is a constant and ![]() . Plainly, instead of solving for
. Plainly, instead of solving for ![]() we can solve a simpler (hopefully) vector and multiply by a constant later.
we can solve a simpler (hopefully) vector and multiply by a constant later.
Let, ![]() , then
, then
(4) 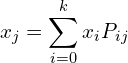
and ![]() . Because
. Because ![]() depends only on
depends only on ![]() and
and ![]() , and using the probabilities from the transition matrix equation (4) becomes,
, and using the probabilities from the transition matrix equation (4) becomes,
(5) ![]()
for, ![]() , starting with
, starting with ![]() and since
and since ![]() ,
, ![]() . Solving equation (5) using the result of
. Solving equation (5) using the result of ![]() starting with
starting with ![]() ,
,
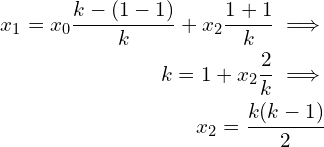
![]() ,
,
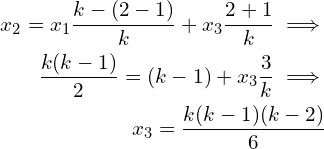
The pattern is clearly
(6) 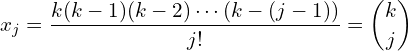
![]() is known,
is known, ![]() can be solved for,
can be solved for,
(7) 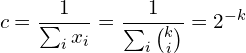
using the fact that ![]() ,
,
(8) 
Final thoughts
The max ![]() is when
is when ![]() . The Ehrenfest model relates to diffusion of matter and heat, intuitively, objects reach some sort of equilibrium but the importance of Ehrenfest model is that there are still fluctuations between all
. The Ehrenfest model relates to diffusion of matter and heat, intuitively, objects reach some sort of equilibrium but the importance of Ehrenfest model is that there are still fluctuations between all ![]() .
.
For example, in the ![]() case you would expect for the long term probability to be peaked at
case you would expect for the long term probability to be peaked at ![]()

With no surprise, the long term probability of the two urns have 10 marbles in each.
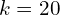 marbles, where both urns contain
marbles, where both urns contain 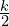
As with ergodic systems, there are fluctuations, between the states of ![]() , as
, as ![]() increases, the probability of have less of a variance. When
increases, the probability of have less of a variance. When ![]() ,
, ![]() becomes very sharply peaked
becomes very sharply peaked
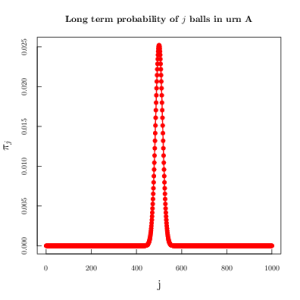
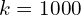 ,
, 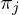 becomes sharply peaked.
becomes sharply peaked.This example should always be appreciated as a basic and straight forward way for the distribution of microstates in physical systems. Large systems (![]() particles, or marbles) become difficult for physical intuition. Paul Ehrenfest, being steeped in the fundamentals of statistical mechanics, knew that systems in equilibrium have a low probability. For instance, the probability of
particles, or marbles) become difficult for physical intuition. Paul Ehrenfest, being steeped in the fundamentals of statistical mechanics, knew that systems in equilibrium have a low probability. For instance, the probability of ![]() is
is ![]() . To put into perspective, there are
. To put into perspective, there are ![]() possible decks of cards. The reader has better odds of guessing the order of 5 fully shuffled deck of cards than the long run probability of the Ehrenfest model being in state
possible decks of cards. The reader has better odds of guessing the order of 5 fully shuffled deck of cards than the long run probability of the Ehrenfest model being in state ![]() , i.e. all the marbles being in urn A.
, i.e. all the marbles being in urn A.
Mark Kac called it “one of the most instructive models in the whole of physics” and to me there is no better example of the sharp distributions of physical systems in equilibrium, and sharp distributions being essential mathematical representation of statistical mechanics.