Derivation of the 1-D Heat Equation and Basic Numerical Methods
When I took a course in Large Scale Computation at Tulane University, I learned a lot and forgot a lot. Understanding how to take a physical phenomena or problem and develop software that is scalable and highly parallelizable, along with optimizing the software for the High Performance Computing (HPC) resources available is enough information to justify a whole degree, so trying to learn all of that in the semester courses that are taught on HPC (if at all) can feel like drinking water from a fire hose. In going back over the class notes I re-remembered one of problems that encompasses all the important parts for scientific computing on HPC resources and in relearning it felt like it would be a great example for beginners to work through.
Heat equation
The heat equation is one of the most well known and simplest partial differential equations (PDEs). The physical intuition and solving the heat equation provides the fundamentals for other equations throughout mathematics and physics. The heat equation and other diffusive PDEs show up throughout statistical mechanics describing random walks and Brownian motion. While the heat equation in 1-D and some other PDEs have analytical solutions, solving most PDEs requires numerical methods to solve.
In this first part of a multi-part series using the example of heat flow in a uniform rod, we’ll go over the physical interpretation of the heat equation, mathematical setup, and discretization for the numerical solution. In later parts of the series we’ll use C++ and open-source parallel computing libraries to solve the problem numerically on HPC resources.
Physical interpretation
From the second law of thermodynamics heat flows from hot to cold proportional to the temperature difference and the thermal conductivity of the material between them. This provides the intuitive result that the rate of heating or cooling is proportional to how much hotter or cooler the surrounding area is.
Conservation of heat
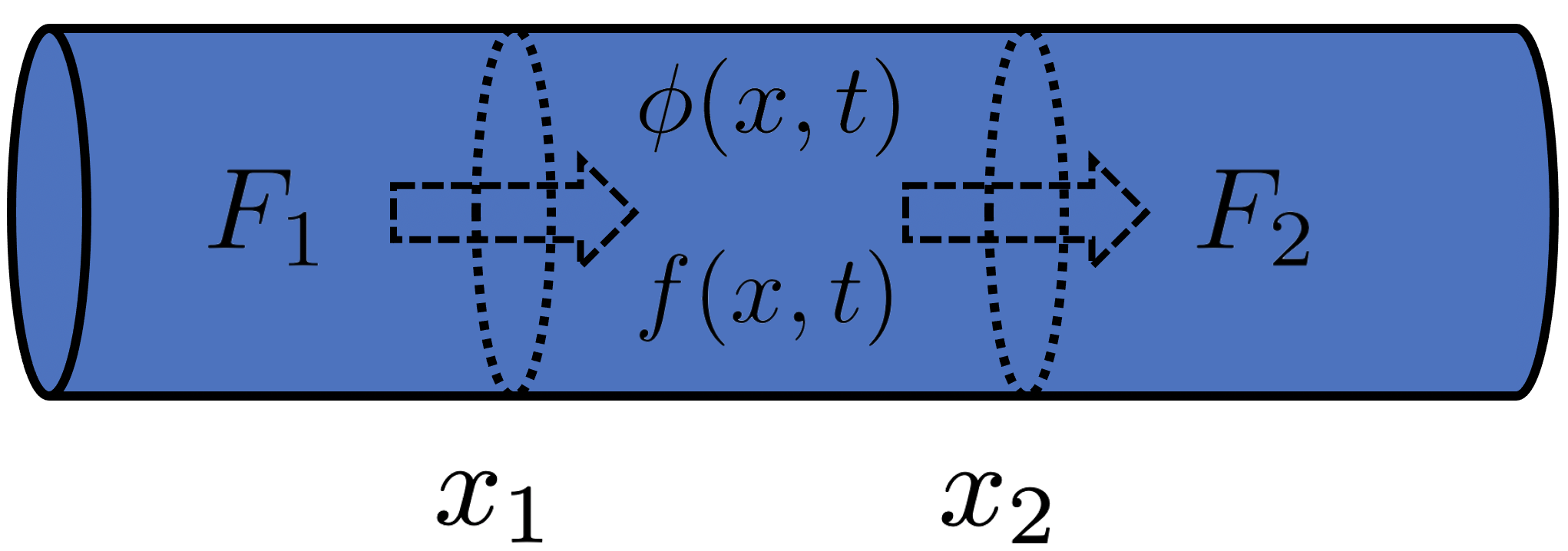
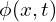 is some conserved quantity,
is some conserved quantity, 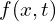 is a source term, and
is a source term, and 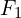 and
and 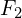 are the flux at
are the flux at 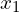 and
and 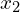 , respectively.
, respectively.
Here we have a conserved quantity, ![]() where
where ![]() might be heat or mass. The total amount of this conserved quantity in an interval
might be heat or mass. The total amount of this conserved quantity in an interval ![]() is defined as,
is defined as,
(1) 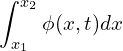
To describe how the amount changes with time over the same interval,
(2) 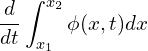
Because ![]() is a conserved quantity, Eq. (2) has to balance with the flux at the boundaries,
is a conserved quantity, Eq. (2) has to balance with the flux at the boundaries, ![]() and
and ![]() , and the generation/consumption term
, and the generation/consumption term ![]() within the interval,
within the interval,
(3) 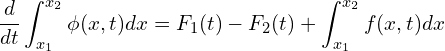
Using Fick’s Law, the flux is proportional to the gradient, ![]() , where
, where ![]() is a constant related to the diffusivity of the material. Using Fick’s Law with Eq. (3),
is a constant related to the diffusivity of the material. Using Fick’s Law with Eq. (3),
![Rendered by QuickLaTeX.com \begin{equation*} \frac{d}{dt} \int_{x_1}^{x_2} \phi (x,t) d x = -\left[-\mathcal{D} \frac{\partial}{\partial x}\phi (x,t) \right ]^{x_2}_{x_1}+ \int_{x_1}^{x_2}f(x,t) d x \implies \end{equation*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-9b553ed19261039e21e96a80cee3419f_l3.png)
(4) 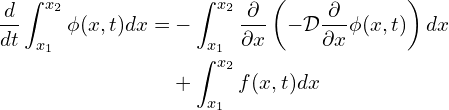
Leibniz integral rule
Using the Leibniz integral rule, we can differentiate under the integral sign of the left side of Eq. (4). The Leibniz integral rule states that for a multivariate function ![]() (here
(here ![]() is a function of
is a function of ![]() and
and ![]() and not the generation/consumption term related to the physical problem) on the interval
and not the generation/consumption term related to the physical problem) on the interval ![]() the derivative of the integral
the derivative of the integral ![]() can be expressed as,
can be expressed as,
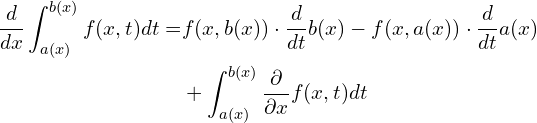
Often the above simplifies into,
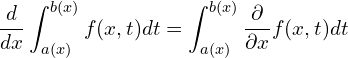
Because the boundary conditions, ![]() and
and ![]() are constants and their derivative will be 0.
are constants and their derivative will be 0.
Final formulation
Applying the Leibniz integral rule with Eq. (4),
(5) 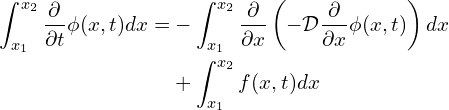
And because all terms of Eq. (5) have the same limits of integration and same differential it can be simplified to,
(6) 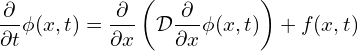
Steady-state with Dirichlet boundary condition
For steady-state the time derivative of ![]() is zero, the equation can be reduced to,
is zero, the equation can be reduced to,
(7) 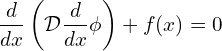
With the Dirichlet boundary conditions of ![]() and
and ![]() .
.
Finite difference method
To evaluate the steady-state heat equation numerically, Eq. (7) must be discretized. This is done approximating the derivative ![]() evaluated at a point
evaluated at a point ![]() to a finite difference between the two nodes outside of the derivative being approximated,
to a finite difference between the two nodes outside of the derivative being approximated, ![]() and
and ![]() , and the “infinitesimal” distance between the two nodes
, and the “infinitesimal” distance between the two nodes ![]() .
.
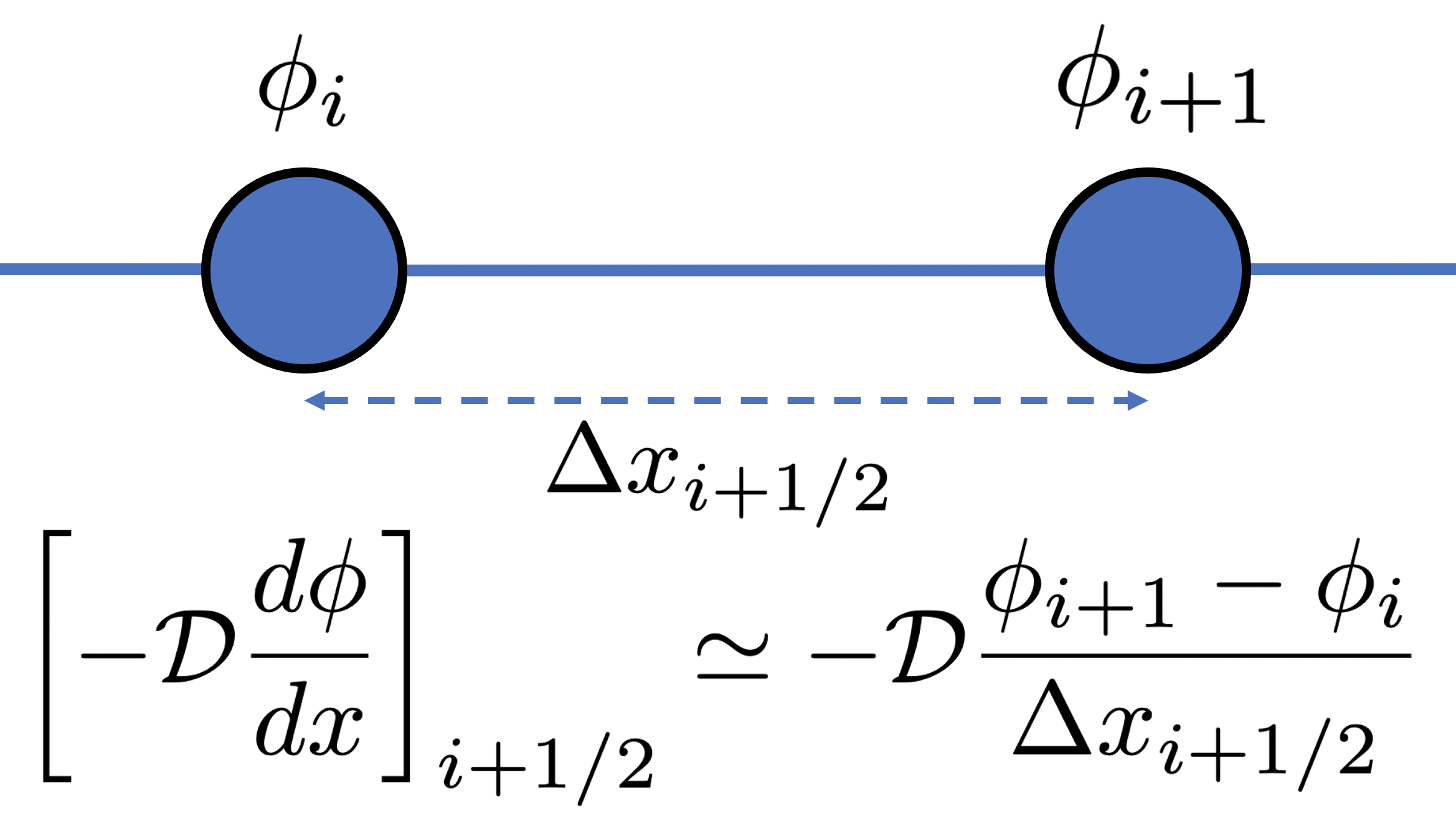
![Rendered by QuickLaTeX.com \left [ -\mathcal{D} \frac{d \phi}{d x} \right ]](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-fed9ac3450130e3ebea5a7e559172055_l3.png) evaluated at
evaluated at 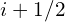 can be approximated by difference between
can be approximated by difference between 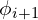 and
and 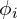 divided by the spacing between the
divided by the spacing between the 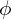 s,
s, 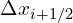 .
.Again using Fick’s Law, the flux is equal to the gradient, we can now use the central difference by substituting the flux, ![]() , into Eq. (7),
, into Eq. (7),
(8) ![]()
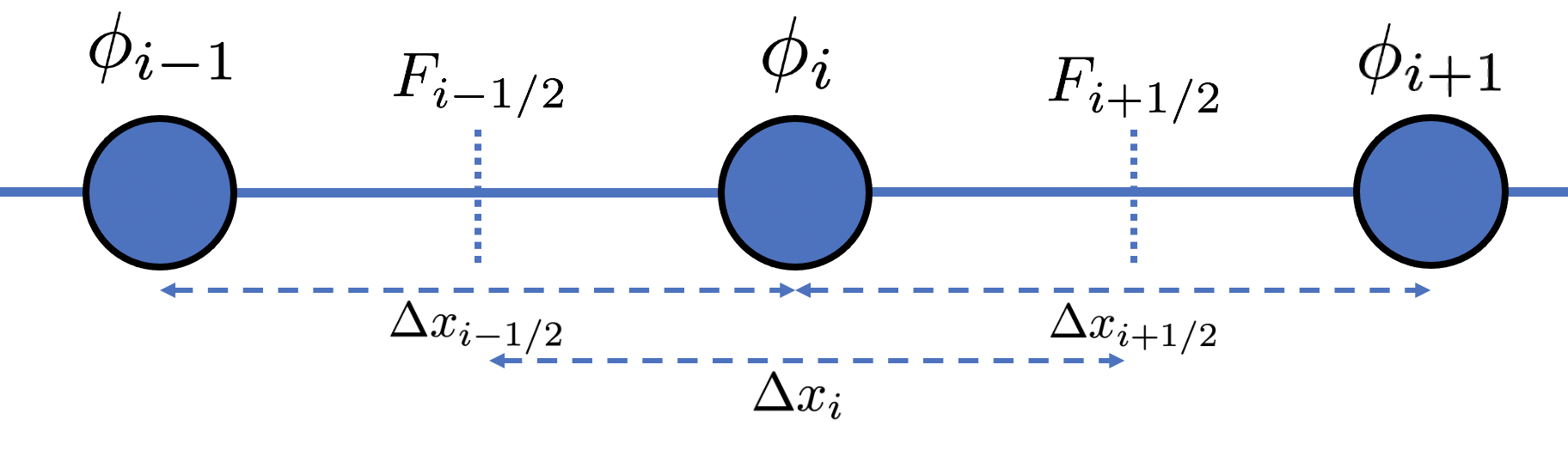
The central difference of the flux,
![Rendered by QuickLaTeX.com \begin{equation*} -\left [ \frac{d F}{d x} \right ]_{i} \simeq - \frac{F_{i+1/2} - F_{i-1/2}}{\Delta x_i} \end{equation}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-28a3dda3c182d60585f8630b29629bcb_l3.png)
And since,
![Rendered by QuickLaTeX.com \begin{equation*} F_{i+1/2} = \left [ -\mathcal{D} \frac{d \phi}{d x} \right ]_{i+1/2} \simeq -\mathcal{D}\frac{\phi_{i+1} - \phi_{i}}{\Delta x_{i+1/2}} \end{equation*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-559d06de7158a946620604e887b5c0ed_l3.png)
and,
![Rendered by QuickLaTeX.com \begin{equation*} F_{i-1/2} = \left [ -\mathcal{D} \frac{d \phi}{d x} \right ]_{i-1/2} \simeq -\mathcal{D}\frac{\phi_{i} - \phi_{i-1}}{\Delta x_{i-1/2}} \end{equation*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-4d2d5804c6068e79d28e81f56221e6e4_l3.png)
The discrete form of Eq. (8) is,
(9) ![Rendered by QuickLaTeX.com \begin{equation*} \frac{\mathcal{D}}{\Delta x_i}\left [ \frac{(\phi_{i+1}-\phi_i)}{\Delta x_{i+1/2}} - \frac{(\phi_{i}-\phi_{i-1})}{\Delta x_{i-1/2}} \right ]+ f(x_i) = 0 \end{equation*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-2b91c343cbf41459094d56c390c55676_l3.png)
And if ![]() and
and ![]() is uniform Eq. (9) simplifies into,
is uniform Eq. (9) simplifies into,
(10) ![]()
Numerical grid and linear system
Consider a uniform grid within ![]() ,
,

In this example, the uniform grid has 7 node points and including the boundary conditions the value of ![]() must satisfy the the following linear system of equations,
must satisfy the the following linear system of equations,
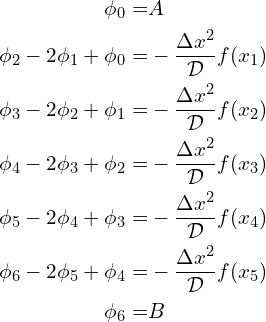
This system of linear system of equations in Matrix-Vector form,
(11) 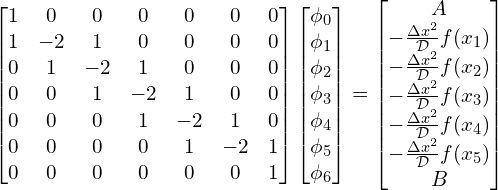
This forms the classic Matrix-Vector equation
(12) ![]()
Where ![]() is a matrix, and both
is a matrix, and both ![]() and
and ![]() are vectors. Through matrix algebra,
are vectors. Through matrix algebra, ![]() can be solved for by computing
can be solved for by computing ![]() .
.
For HPC, and scientific computations in general, it is beneficial for ![]() to be a symmetric matrix. In Eq. (11), the matrix
to be a symmetric matrix. In Eq. (11), the matrix ![]() is close to being symmetric and we can take advantage that
is close to being symmetric and we can take advantage that ![]() and
and ![]() are known but are included in the unknown vector
are known but are included in the unknown vector ![]() . By eliminating
. By eliminating ![]() and
and ![]() from the system of linear equations and the matrix
from the system of linear equations and the matrix ![]() in Eq. (7),
in Eq. (7),
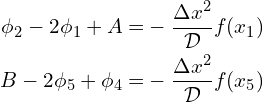
Resulting in,
(13) 
And now ![]() is symmetric. Now that we have our physical problem discretized, and setup in such a way that
is symmetric. Now that we have our physical problem discretized, and setup in such a way that ![]() in
in ![]() , is symmetric we can begin to solve numerically.
, is symmetric we can begin to solve numerically.
Iterative method
When solving for the unknown vector, ![]() , from the linear system of equations from Eq. (12),
, from the linear system of equations from Eq. (12), ![]() is solved with iterative methods, using the sceme,
is solved with iterative methods, using the sceme,
(14) ![]()
Where ![]() and
and ![]() are unknown constant vector matrix and vector and
are unknown constant vector matrix and vector and ![]() is a step that may not satisfy the equation Eq. (12) and
is a step that may not satisfy the equation Eq. (12) and ![]() is the iterative step counter. We begin to solve for
is the iterative step counter. We begin to solve for ![]() , the solution must satisfy the equation,
, the solution must satisfy the equation,
![]()
Solving for ![]() and using the
and using the ![]() ,
,
![]()
The iterative scheme of Eq. (14) is now,
(15) 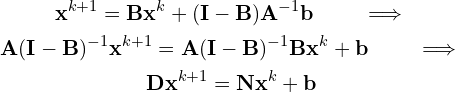
Where ![]() and
and ![]() .
. ![]() can be split as,
can be split as,
(16) ![]()
We arrive at the final equation for computing the unknown vector ![]() is,
is,
(17) ![]()
For an iterative method, computing ![]() and
and ![]() must converge rapidly and be computationally inexpensive.
must converge rapidly and be computationally inexpensive.
Convergence
The error for an iterative method at step ![]() is
is ![]() . The error must also satisfy the equation,
. The error must also satisfy the equation,
(18) ![]()
And converges if,
![]()
Also assuming that ![]() has the eigenvalue equation,
has the eigenvalue equation,
(19) ![]()
The initial error, ![]() using the eigenvectors from Eq. (19) is defined as
using the eigenvectors from Eq. (19) is defined as
(20) ![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{e}^0 := \sum_{i=1}^{\mathrm{rank}\left [ \mathbf{B}\right ]} a_i \mathbf{z}_i \end{equation*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-48f11d62b8a488d99d88b83dc8551dc1_l3.png)
Where ![]() is a constant. Resulting in the formula for
is a constant. Resulting in the formula for ![]() ,
,
(21) ![Rendered by QuickLaTeX.com \begin{equation*} \mathbf{e}^k = \sum_{i=1}^{\mathrm{rank}\left [ \mathbf{B}\right ]} a_i (\lambda_i)^k \mathbf{z}_i \end{equation*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-8c2932cd4a60c388cf4a03ac4fdec38b_l3.png)
If the magnitude of the eigenvalues, ![]() is less than 1,
is less than 1, ![]() converges to 0 as
converges to 0 as ![]() . For convergence the spectral radius of
. For convergence the spectral radius of ![]() ,
, ![]() , must meet the criteria,
, must meet the criteria,
(22) ![]()
For the matrix ![]() from Eq. (12) to have guaranteed convergence the following criteria must be met,
from Eq. (12) to have guaranteed convergence the following criteria must be met,
(23) ![]()
Jacobi Method for the 1-D heat equation
The simplest iterative method is the Jacobi Method. An ![]() matrix
matrix ![]() has a matrix
has a matrix ![]() composed of the diagonal elements of
composed of the diagonal elements of ![]() ,
,
![]()
Computing only inverse of the diagonal elements is fast and easy, resulting in, ![]() . We will define
. We will define ![]() as the off-diagonal elements of
as the off-diagonal elements of ![]() ,
,
![]()
For any iterative method to have guaranteed convergence the spectral radius must follow Eq. (23). The Jacobi Method also provides another sufficient condition of convergence that is,
(24) ![]()
The matrix ![]() from Eq. (13), is clearly diagonally dominant so our unknown vector
from Eq. (13), is clearly diagonally dominant so our unknown vector ![]() will converge as
will converge as ![]() . The diagonal matrix
. The diagonal matrix ![]() ,
,
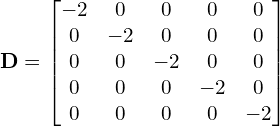
And from Eq. (16) ![]() has the off-diagonal elements of
has the off-diagonal elements of ![]() ,
,
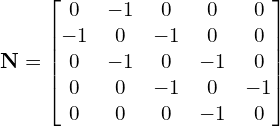
The iterative scheme solving for solving ![]() from Eq. (13) is now,
from Eq. (13) is now,
(25) 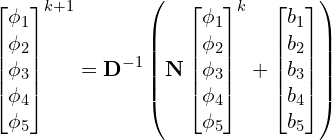
And where ![]() is the number of iterations. The last term
is the number of iterations. The last term ![]() for Eq. (17) is,
for Eq. (17) is,
(26) 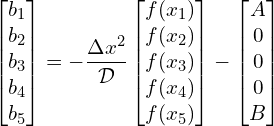
For the Jacobi Method, the general equation to find ![]() at node
at node ![]() after
after ![]() steps is using the matrix
steps is using the matrix ![]() is,
is,
(27) 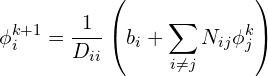
Gauss-Seidel Method
The Gauss-Seidel method is another iterative method. The main difference between Gauss-Seidel and the Jacobi method is that the diagonal matrix, ![]() , is determined by the lower triangle elements of
, is determined by the lower triangle elements of ![]() in Gauss-Seidel is the,
in Gauss-Seidel is the,
(28) ![]()
And now the ![]() matrix contains the upper triangle elements of
matrix contains the upper triangle elements of ![]() ,
,
(29) ![]()
Similar to the Jacobi Method, if the matrix ![]() is diagonally dominant, Gauss-Seidel converges from Eq. (24).
is diagonally dominant, Gauss-Seidel converges from Eq. (24).
Solving the 1-D heat equation’s linear system of equations from Eq. (13) the matrices for Gauss-Seidel become,
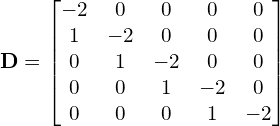
and,
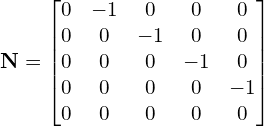
The iterative scheme is again Eq. (17). For Gauss-Seidel the computation for ![]() is more involved than for the Jacobi method. Our system is,
is more involved than for the Jacobi method. Our system is,
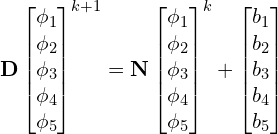
And now,
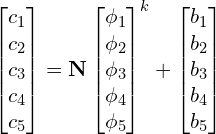
The linear system of equations becomes,
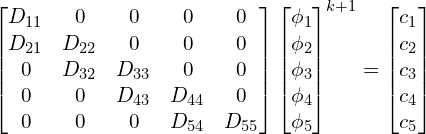
We can solve the general form for ![]() using induction. The first term,
using induction. The first term, ![]() is,
is,
![]()
The second term, ![]() ,
,
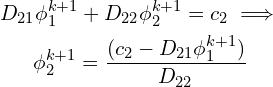
And the third term,
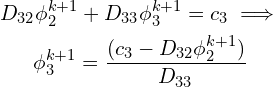
And finally for the ![]() th node at the
th node at the ![]() step the general equation is,
step the general equation is,
(30) 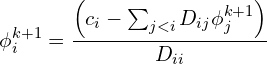
Next in the series
In future posts of this series, we’ll solve this problem numerically using C++ with OpenMP and MPI!