Metropolis-Hastings Algorithm
History of Metropolis-Hastings
One of, if not the most, popular Markov chain Monte Carlo (MCMC) methods is the famous Metropolis-Hastings algorithm. Metropolis-Hastings has its roots grounded in statistical mechanics, and was originally used to calculate the equation of state for simple Lennard-Jones particles in two dimensions. The nature of statistical mechanics produces problems that are difficult analytically, and often times require simulation. Operationally, these simulations need ways to cleverly reduce the number of calculations because there are ![]() interactions between
interactions between ![]() particles and can quickly become intractable as
particles and can quickly become intractable as ![]() becomes large.
becomes large.
Named after Nicholas Metropolis and W. K. Hastings, the algorithm was developed during Nicholas Metropolis’ time at Los Alamos National Laboratory in the Theoretical Division with Arianna W. Rosenbluth, Marshall N. Rosenbluth, Augusta H. Teller while W.K. Hastings expanded the work while a professor at the University of Toronto in the late 60s. While the true development of the algorithm remains contested, its success and utility is without question.
Mathematics behind Metropolis-Hastings
Let ![]() be a discrete probability distribution. The algorithm will construct an irreducible Markov chain, with random variables
be a discrete probability distribution. The algorithm will construct an irreducible Markov chain, with random variables ![]() whose stationary distribution is
whose stationary distribution is ![]() .
.
Let ![]() be a transition matrix for any irreducible Markov chain with the same state space as
be a transition matrix for any irreducible Markov chain with the same state space as ![]() .
. ![]() will be the proposal chain, and generate elements of a sequence of elements that the algorithm decides whether or not to accept.
will be the proposal chain, and generate elements of a sequence of elements that the algorithm decides whether or not to accept.
To describe the transition mechanism for ![]() , we assume that at time
, we assume that at time ![]() , the chain is at
, the chain is at ![]() ,
, ![]() . Then,
. Then, ![]() is determined by the two-step procedure:
is determined by the two-step procedure:
- Choose a new state according to
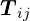 , or more plainly propose
, or more plainly propose 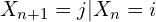 .
. - Decide whether to accept a move to
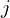 or not using an acceptance function. Let
or not using an acceptance function. Let
(1) 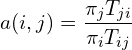
If ![]() then
then ![]() is accepted as the next state of the chain. If
is accepted as the next state of the chain. If ![]() , then
, then ![]() is accepted with probability
is accepted with probability ![]() . Operationally,
. Operationally, ![]() is accepted through the direct comparison with a random variable,
is accepted through the direct comparison with a random variable, ![]() , selected from the uniform distribution
, selected from the uniform distribution ![]() on the interval
on the interval ![]() . Assume,
. Assume, ![]() , then
, then
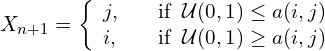
That’s the Metropolis-Hastings algorithm. Some things to note and to take advantage of:
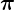 does not need to be known. The reason is that we only need to know
does not need to be known. The reason is that we only need to know 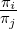 , this is useful when
, this is useful when 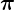 is uniform because the acceptance function simplifies to
is uniform because the acceptance function simplifies to 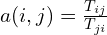 .
.- When the transition matrix,
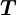 , is symmetric the acceptance function is
, is symmetric the acceptance function is 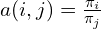
Metropolis-Hastings examples in R
Discrete space
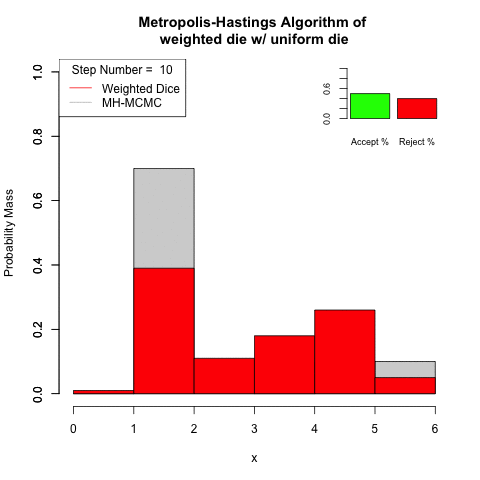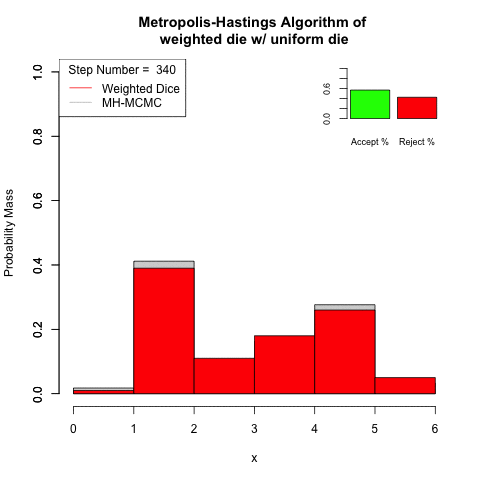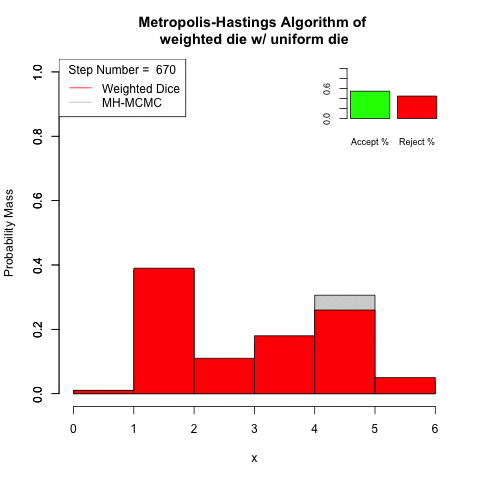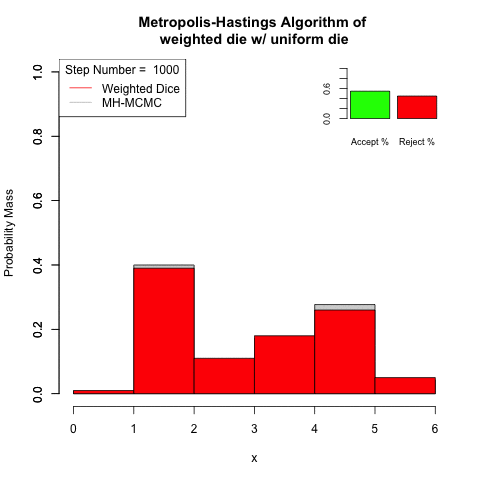
Use the Metropolis-Hastings algorithm to sample from a weighted-die with the distribution
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0.01 | 0.39 | 0.11 | 0.18 | 0.26 | 0.05 |
Using an even die, as the proposal step.
The stationary distribution is obviously, ![]() and the transition matrix,
and the transition matrix, ![]() , is the roll of a fair die. The transition matrix in this case is uniform, i.e.
, is the roll of a fair die. The transition matrix in this case is uniform, i.e. ![]() for all
for all ![]() and
and ![]() . The equation for acceptance function (1) then simply becomes,
. The equation for acceptance function (1) then simply becomes,
![]()
The problem can be easily implemented using your favorite programming language. The following is a solution in R.
The simulated Markov chain converges to the stationary distribution quickly.
Continuous space
Show how to use the Metropolis–Hastings algorithm to simulate from the double-exponential distribution, with density
![]()
The stationary distribution ![]() is
is ![]() , from state
, from state ![]() , the proposal chain moves to
, the proposal chain moves to ![]() , where
, where ![]() is normally distributed. The conditional density given
is normally distributed. The conditional density given ![]() is constant, with
is constant, with
![]()
The acceptance function is
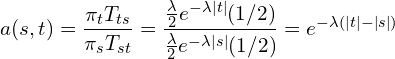
Again, the implementation in R
Generally, simulated continuous space Markov chains require more steps for convergence.
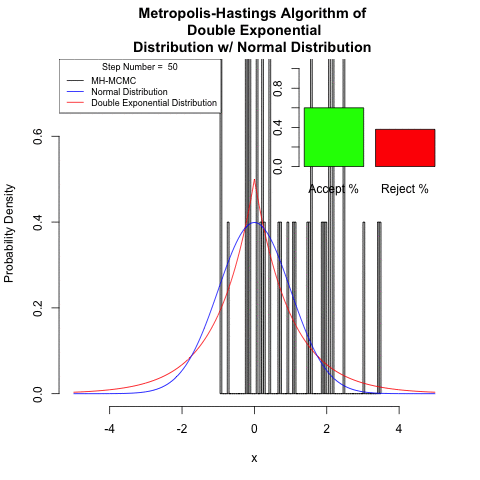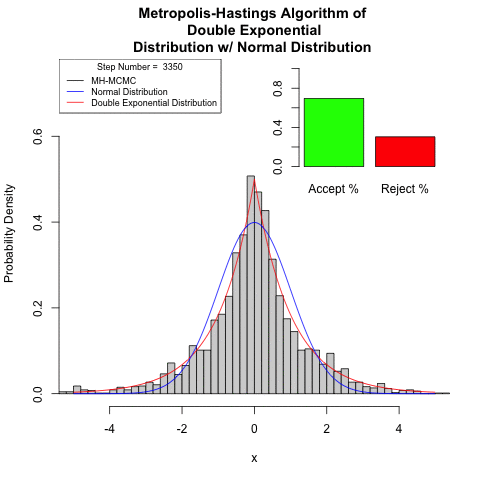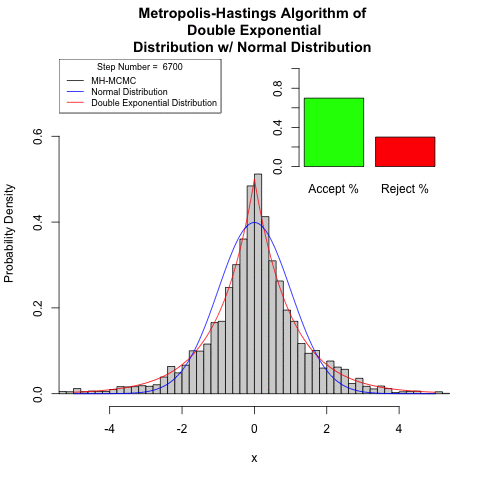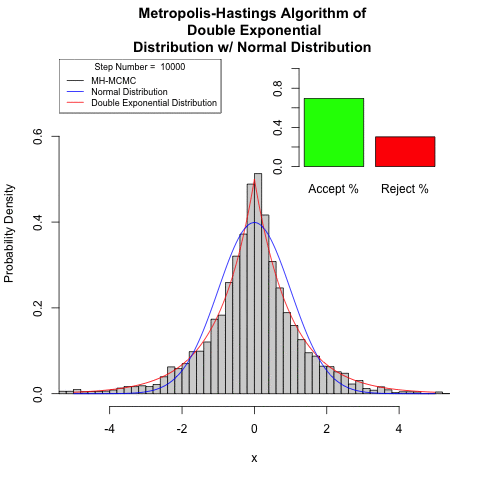
Final Thoughts
These basic examples show the utility of the Metropolis-Hastings algorithm. MH uses an incredibly simple and clear way to solve difficult problems. Those problem, “How do I simulate a difficult distribution, using a simple, well established, distribution?” and “How can cleverly reduce the number of calculations in physical systems?”.