Capillary bridges
Capillary bridges are the minimized surface between two rigid bodies. My interest is in studying small drops of water between a two chemically distinct plates, where the one plate might be hydrophilic and the other might be hydrophobic. The resulting shape and physical phenomena are important in understanding the forces between this droplet and the plates. While the scales of capillary bridges are small the relative forces can be strong and complex. The classic examples of these forces would be if you put water between two plates of glass and tried to pull them apart. The surface of glass has a low contact angle for water (hydrophilic) making it difficult to separate these two plates. The ancient Egyptians took advantage of capillary bridges in the building of the pyramids. They would pour water on sand under the stone blocks as they would move them. The pillar surface of the sand creates a high contact angle for water (hydrophobic) and lowers the friction between the blocks and the sand making it easier to move.
In working up to solving the forces of capillary bridges, here we solve minimal surface problem. This provides a “gentle” introduction to variational calculus.

https://www.platypustech.com/
Minimal surface and soap film

The classic problem used to illustrate the minimal surface problem is through soap film. You might have done this as a kid, at the local children’s museum (shoutout Explora) they had two wire rings that you could cover with a soap film. The resulting shape is called a catenoid and is the minimization of the surface area. Using variational calculus, and basic computations we can solve the minimal surface problem.
Soap film
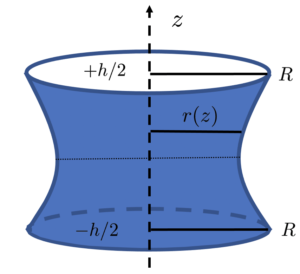
 , separated by a distance
, separated by a distance 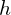 .
.Consider two metal wires, with radius ![]() , oriented perpendicular to the
, oriented perpendicular to the ![]() -axis and separated by a distance
-axis and separated by a distance ![]() . A soap film captured between two parallel plates is assumed to be cylindrically symmetric about the
. A soap film captured between two parallel plates is assumed to be cylindrically symmetric about the ![]() -axis. We want to determine the droplet shape. The free energy of this droplet
-axis. We want to determine the droplet shape. The free energy of this droplet ![]() , is a product of the surface tension and the surface,
, is a product of the surface tension and the surface, ![]() . To minimize the free energy we minimize the surface.
. To minimize the free energy we minimize the surface.
The surface can be calculated through integrating surface element ![]() across the height of the bridge,
across the height of the bridge,
(1) 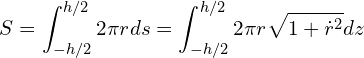
Where ![]() and instead of integrating over the surface element
and instead of integrating over the surface element ![]() , we integrate over the arc length. Similar to “elementary” calculus the derivative at the extremum in variational calculus is also 0,
, we integrate over the arc length. Similar to “elementary” calculus the derivative at the extremum in variational calculus is also 0, ![]() where
where ![]() is small variations in
is small variations in ![]() . We now compute,
. We now compute,
(2) 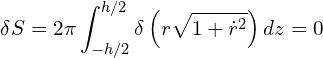
Using the product rule,
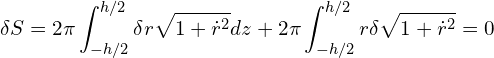
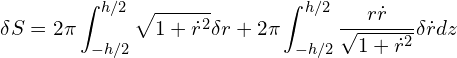
We need to integrate by parts on the second term of the equation so all terms are in variation of ![]() and not
and not ![]() ,
,
![Rendered by QuickLaTeX.com \begin{equation*} \begin{split} \int_{-h/2}^{h/2} \frac{r \dot{r}}{\sqrt{1 + \dot{r}^2}} \delta \dot{r} =&\left . \left [ \frac{r \dot{r}}{\sqrt{1 + \dot{r}^2}} \delta \dot{r} \right ]\right|_{-h/2}^{h/2} \\ &-\int_{-h/2}^{h/2} \frac{d}{dz}\left ( \frac{r \dot{r}}{\sqrt{1 + \dot{r}^2}} \right ) \delta r dz \end{split} \end{equation*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-0a2e0032c33d38e96a58b16b2239e2fa_l3.png)
We can cancel out the terms in bracket from the boundary conditions, ![]() , resulting in,
, resulting in,
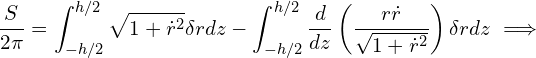
(3) 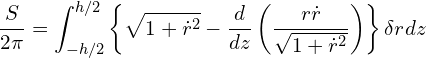
To minimize ![]() , the term in the braces must be 0.
, the term in the braces must be 0.
(4) 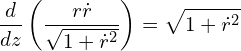
Carrying out of derivative,
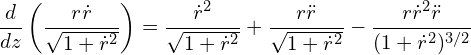
Combining with Eq. (4),
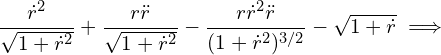
![]()
(5) ![]()
Solving Eq. (5) can be solved by multiplying by ![]() and the resulting can then be written as,
and the resulting can then be written as,
(6) 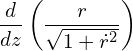
The solution to minimization reduces to solving,
(7) ![]()
where ![]() is a constant of integration. Eq. (7) is an easily solved first-order nonlinear differential equation. We start by,
is a constant of integration. Eq. (7) is an easily solved first-order nonlinear differential equation. We start by,
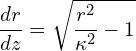
and now through separations of variables,
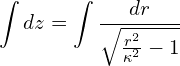
Finally, substituting ![]() ,
,
![]()
And at ![]() , resulting in
, resulting in
(8) ![]()
Now at the boundary conditions, ![]() and
and ![]() ,
,
![]()
Because ![]() is an even function, either
is an even function, either ![]() or
or ![]() . The first case,
. The first case, ![]() is inconsistent, so we use the second
is inconsistent, so we use the second ![]() , thus,
, thus,
(9) ![]()
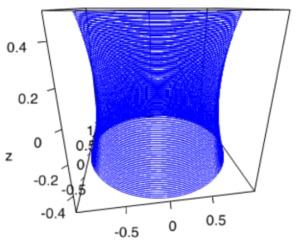
Example soap film in R
Here we analyze the solution for a soap film between two wire rings of radius, ![]() , and separated by a distance of
, and separated by a distance of ![]() . We now try to find the
. We now try to find the ![]() that satisfy the Eq. (9) at the boundary conditions,
that satisfy the Eq. (9) at the boundary conditions,
![]()
![]()
The critical values are ![]() and
and ![]() provide a solution for a stable catenoid, which is the minimal surface and an unstable surface where the bridge will pop.
provide a solution for a stable catenoid, which is the minimal surface and an unstable surface where the bridge will pop.
Stable catenoid
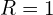 and
and 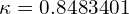 .
.Unstable catenoid
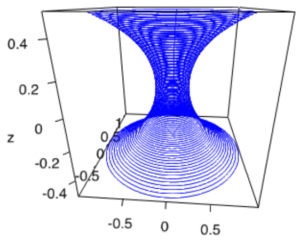
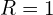 and
and 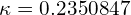 .
.R code