Bernoulli-Laplace
The Bernoulli-Laplace model of diffusion describes the flow of two incompressible liquids between two containers. It may be described as two urns that contain ![]() balls each. Initially, the balls in the left urn are all red and the balls in the right urn are all blue. At each step, pick a ball at random from each urn and exchange them so that each box always contains
balls each. Initially, the balls in the left urn are all red and the balls in the right urn are all blue. At each step, pick a ball at random from each urn and exchange them so that each box always contains ![]() balls. Let
balls. Let ![]() be the number of blue balls in the left urn at step
be the number of blue balls in the left urn at step ![]() , find the transition matrix, and the stationary distribution,
, find the transition matrix, and the stationary distribution, ![]() .
.

Transition Matrix
Initially, ![]() and the complete state space of
and the complete state space of ![]() . Furthermore, to understand the transition matrix, the transition probabilities,
. Furthermore, to understand the transition matrix, the transition probabilities, ![]() , between states must be known.
, between states must be known.
Suppose ![]() , there are 4 possible outcomes to
, there are 4 possible outcomes to ![]() from
from ![]() of any given step:
of any given step:
- Blue from the left and blue from the right with probability
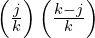 giving
giving 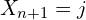 .
. - Blue from the left and red from the right with probability
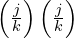 giving
giving 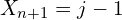 .
. - Red from the left and red from the right with probability
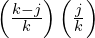 giving
giving 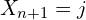 .
. - Red from the left and blue from the right with probability
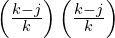 giving
giving 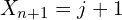 .
.
Moreover, these outcomes can be shown as,
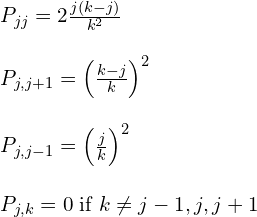
Consequently, the complete transition matrix,

Stationary distribution
Similar to the Ehrenfest urn model that was solved previously, the long term probability that ![]() blue marbles are in the left urn is an essential question to be solved.
blue marbles are in the left urn is an essential question to be solved.
To begin with, ![]() and
and ![]() (using
(using ![]() ). Next, for
). Next, for ![]() ,
,
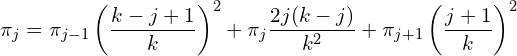
Incidentally, ![]() , can be written as
, can be written as ![]() . Next solve using induction,
. Next solve using induction,
![Rendered by QuickLaTeX.com \begin{align*} \pi_{j+1} &= \left ( \frac{k}{j+1} \right )^2 \left [ \pi_j - \pi_{j-1} \left (\frac{k-j + 1}{k} \right )^2 - \pi_j \frac{2j(k-j)}{k^2} \right ] \\ &= \left ( \frac{k}{j+1} \right )^2 \left [ {k \choose j} ^2 - {k \choose {j -1}}^2 \left (\frac{k-j + 1}{k} \right )^2 \right \\ &\qquad \left - {k \choose j}^2 \frac{2j(k-j)}{k^2} \right ] \pi_0 \\ &=\left ( \frac{k}{j+1} \right )^2 \left [ {k \choose j} ^2 - \frac{1}{k^2} \left ( \frac{k!}{(k-j)!(j-1)!} \right )^2 \\ \right & \qquad \left - {k \choose j}^2 \frac{2j(k-j)}{k^2} \right ] \pi_0 \\ &= \left ( \frac{k}{j+1} \right )^2 {k \choose j} ^2 \left [ 1 - \frac{j^2}{k^2} - \frac{2 j(k-j)}{k^2} \right ] \pi_0\\ &=\left ( \frac{k}{j+1} \right )^2 {k \choose j} ^2 \left [ \frac{k^2 - j^2 -2 j k -2 j^2}{k^2} \right ] \pi_0\\ &= \pi_0 \left ( \frac{k!}{(k-j)!(j+1)!} \right ) ^2 (k-j)! \implies \\ \pi_{j+1} &= \pi_0 { k \choose j+1 } \end{align*}](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-570b6c32da12e5f583510cae03dd982c_l3.png)
Since, ![]() and
and ![]() ,
,
![Rendered by QuickLaTeX.com \[\pi_0 = \left [ \sum_{j=0}^k {k \choose j } ^2 \right ] ^{-1} = {2k \choose k}\]](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-3134cf6856b4eb6cf366221ae3c04514_l3.png)
Finally, the unique limiting distribution for the Bernoulli-Laplace Urn model
![Rendered by QuickLaTeX.com \[\pi_j = {k \choose j}{2k \choose k}^{-1}\]](https://www.diegogomez.studio/wp-content/ql-cache/quicklatex.com-6bc2db7ae48fe1c6f4dfc37b9d23fa07_l3.png)
As a final point it’s important to note that the final form of ![]() requires a good understanding of combinatorics and lots of scratch paper to simplify. Save for Bernoulli and Laplace like intuition of these types of problems, it is difficult to recognize the mathematical trick to write
requires a good understanding of combinatorics and lots of scratch paper to simplify. Save for Bernoulli and Laplace like intuition of these types of problems, it is difficult to recognize the mathematical trick to write ![]() and work from there.
and work from there.